近日,由国家自然科学基金委员会资助,徐州工程学院与兰州大学联合承办的“反应扩散方程理论及其应用讲习班”顺利举办。活动采取线上、线下相结合的方式进行,吸引了来自全国100余所高校的600余名学员线上参加学习,线下学习学员超过100人,全面共享学术盛宴。
线上学习
开班仪式由徐州工程学院数学与统计学院院长苏有慧主持,副校长谭文轶出席并致欢迎辞。谭校长在致辞中介绍了学校的发展情况,并希望通过此次讲习班进一步推动数学学科与相关领域的交流合作,激发青年学者的创新意识与科研潜力。
开班仪式致辞
本次讲习班共设置4门课程,其中线上专题课程2门:
香港理工大学王治安教授讲授《带有密度依赖扩散机制的反应扩散方程》,围绕具有密度依赖扩散机制的趋化模型与细菌运动模型展开深入讲解,聚焦临界质量问题中的整体解存在性与爆破解,以及密度抑制扩散机制下模型的适定性与稳定性分析。课程内容涵盖整体解的存在与唯一性、解的全局稳定性、非线性扩散对模式形成的影响及其数学刻画,揭示了该类模型在生命科学和复杂系统建模中的理论意义与应用价值。
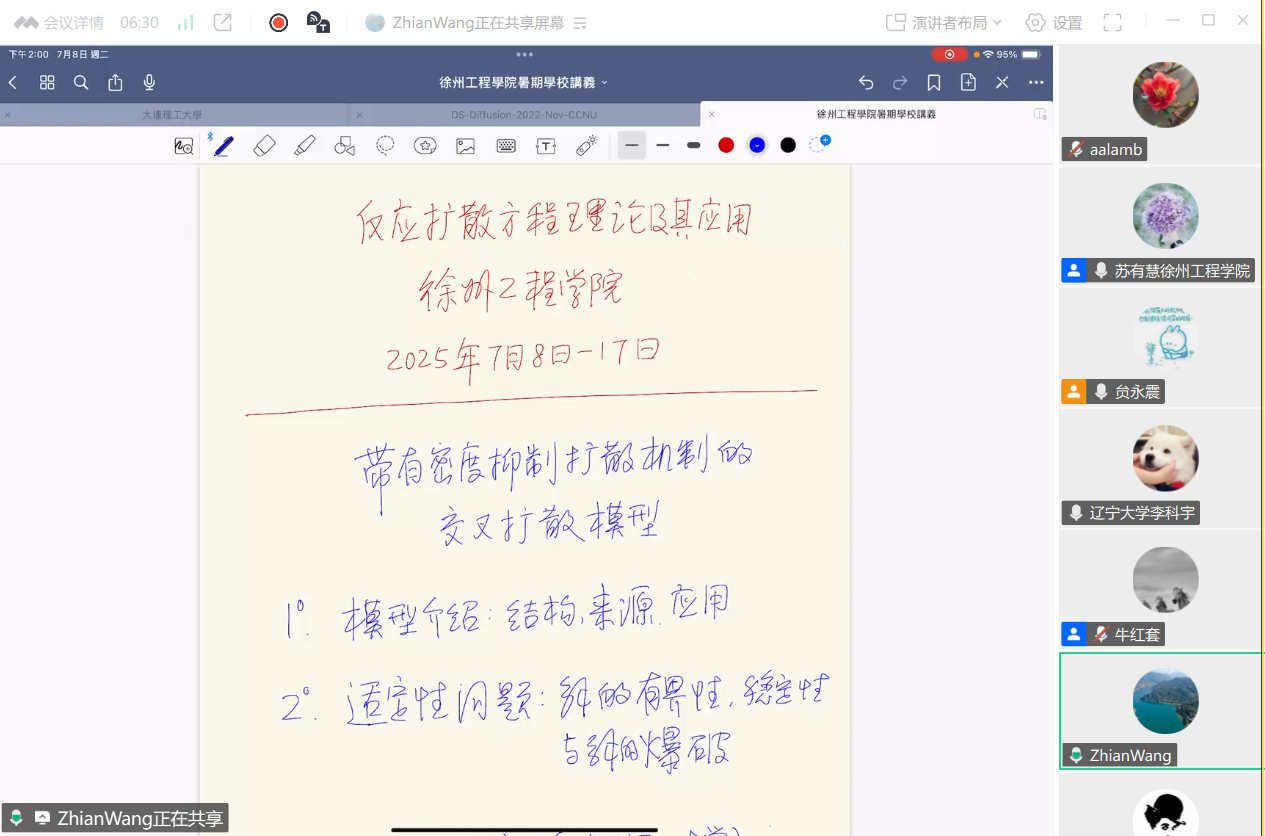
线上专题课1
威廉玛丽学院史峻平教授讲授《生物数学中的反应扩散模型与分歧理论》,围绕反应扩散方程组中的稳态与动态行为,系统讲解了Banach空间下稳态问题的隐函数定理、鞍结点分歧、跨越分歧、音叉分歧等典型分歧类型,深入分析了紧算子与Fredholm算子下全局分歧理论在反应扩散方程组中的应用。内容涵盖Turing不稳定性引发的空间模式、Hopf分歧产生的周期解、时空结构演化机制,以及球对称解的个数与分歧图构造,展示了反应扩散模型在理论生物学中的广泛适用性与深刻数学结构。
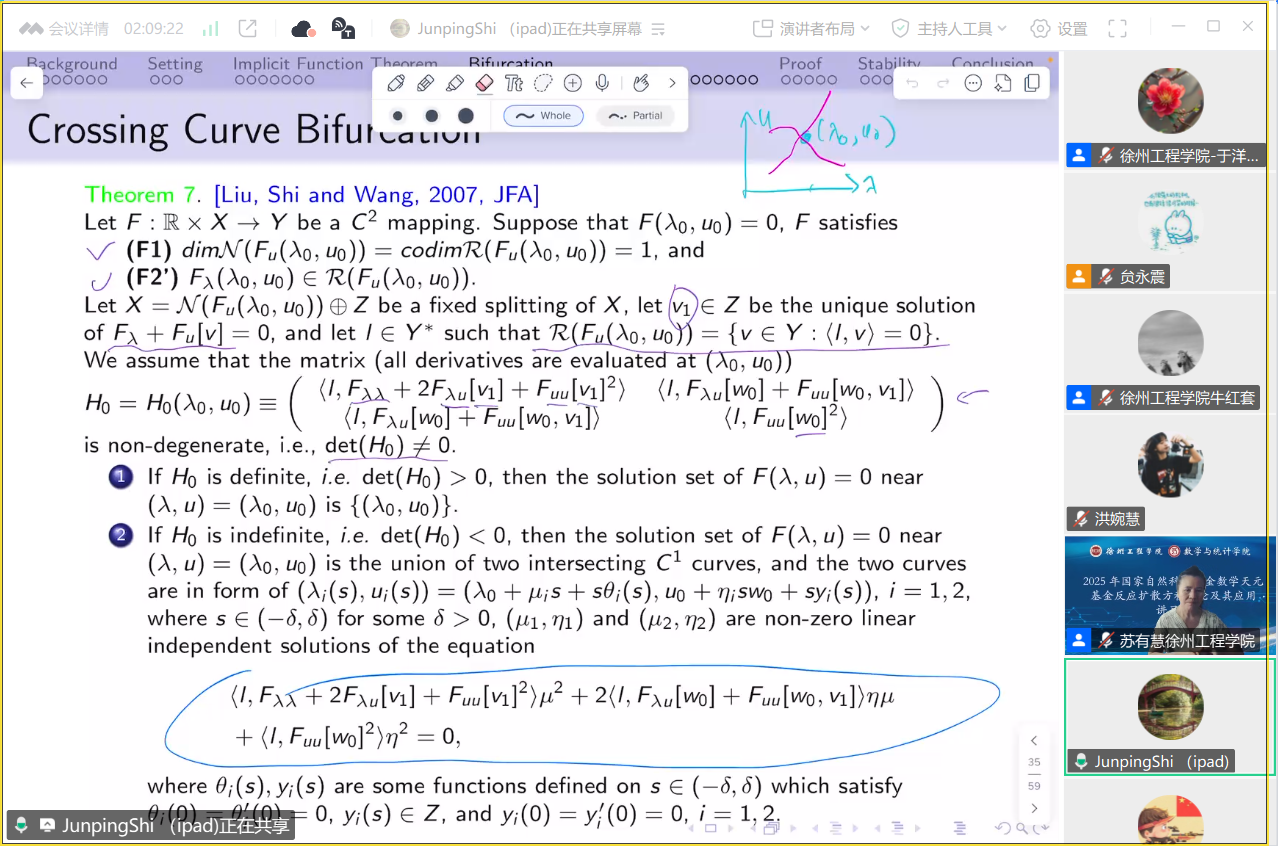
线上专题课2
线下基础课程2门:
南京大学钟承奎教授讲授《非线性泛函分析中的拓扑方法》,系统讲解了非线性泛函分析中的经典拓扑方法,内容涵盖Sard定理、Brouwer度与不动点定理、Borsuk定理、Leray-Schauder度及其在紧同伦与不动点问题中的应用。进一步引入Banach空间中的半序与锥结构,讲解Krein-Rutman定理及锥映射的拓扑度理论,探讨非线性微分方程(尤其是椭圆型方程)解的存在性与多解性问题,为学员深入理解变分方法和拓扑方法在偏微分方程中的应用奠定了坚实基础。


线下基础课1
山西大学王明新教授讲授《二阶抛物方程基本理论与方法》,系统讲解了二阶抛物方程解的估计理论(包括Lp估计、 Schauder估计)、极值原理、正则性理论及解的一致估计。课程内容还涵盖了解的局部存在与唯一性、上下解方法以及稳定性分析等,全面展示了抛物方程从局部理论到全局性质的研究路径,为深入研究偏微分方程打下坚实基础。


线下基础课2
此次讲习班不仅为青年教师和研究生提供了高水平学习平台,也有力促进了反应扩散方程理论及其应用研究的交叉融合与创新发展,对推动数学领域复合型人才培养具有重要意义。
文字图片:于洋洋 马陆一
初审:牛红套
复审:王豹
终审:苏有慧
